零知識證明的基礎介紹及其在區塊鏈領域的應用_PRO:LON

在復雜的密碼學領域，零知識證明為一項看似矛盾的任務提供了獨特的解決方案：在不透露信息本身的情況下證明知道某一信息。這種加密方法涉及兩方：證明者及驗證者。證明者的目的是證明他們擁有某一信息（我們稱之為x），而不透露任何關于x本身的數據。驗證者則從交流中了解到的只是證明者擁有這種知識的簡單事實。最重要的是，驗證者并沒有獲得關于x的額外信息。

比如當小零與小十在玩密室逃脫，此時小零告訴小十他已經破解了某“寶箱”的密碼。但是小零不愿意直接分享現成的“答案”，也不愿當著小十的面將寶箱打開。那么怎樣證明給小十，他真的破解了迷題并且知道寶箱密碼呢？

于是他讓小十在一張紙上寫一段只有自己知道的字符串，同時簽上自己名字，將紙張從寶箱的縫隙中塞了進去。

隨后小零打開寶箱取出了小十放進去的紙張，并展示給了小十看，小十核對字符串和簽名無誤。這證明了小零確實知道寶箱密碼，而且這張紙確實是寶箱里拿出來的。

該解密過程既沒有被小十知曉，同時小零又證明了他已破解了寶箱密碼。

零知識證明

密碼學中，零知識證明（Zero Knowledge Proof，也稱ZKP）或零知識協議是一種方法，該方法可令證明者在不透露信息本身或其他任何信息的情況下，讓驗證者相信或證明給驗證者某個陳述或論斷的真實性。

SKALE即將發布去中心化零知識證明解決方案Levitation Protocol:6月2日消息，以太坊側鏈 SKALE 開發人員宣布了一項 SKALE 改進提案，即，去中心化零知識證明解決方案 Levitation Protocol，旨在通過使全套 ZK 解決方案無縫連接到 SKALE 架構，并將 Rollup 連接到以太坊主網。該提案包括進一步的生態系統升級，增加了一個新的「Layer 1 Megachain」，稱為 SKALE G（G 代表木衛三，太陽系中最大的衛星）。

SKALE 開發人員計劃在未來幾個月內開始發布 Levitation Protocol 源代碼，之后將啟動公共測試網。Levitation Protocol 主網計劃于 2023 年第四季度推出。[2023/6/2 11:53:31]

零知識證明最初是于由麻省理工教授Shafi Goldwasser、Silvio Micali以及密碼學大師Charles Rockoff三位作者在《The Knowledge Complexity of Interactive Proof Systems》論文中提出的。該一算法概念為現代密碼學奠定了一定基礎。

零知識證明有兩個額外的屬性：簡明性和零知識。簡明性允許驗證者接受一個大型計算的正確性，而無需自己計算該語句或陳述。而零知識保證了沒有任何關于輸入的數據被泄露。

MolochDAO推出基于零知識證明的“隱私池”加密混合服務:3月7日消息，為以太坊基礎設施項目提供資金支持的去中心化自治組織MolochDAO推出基于零知識證明的“隱私池”加密混合服務，旨在保護鏈上交易時的隱私，同時還允許用戶證明他們遵守當地法規。

據悉，MolochDAO的隱私池（Privacy Pools）將利用零知識證明這一隱私保護技術，使用戶能夠證明他們正在將受制裁的錢包列入黑名單，同時無需透露他們是誰，也無需披露全部交易歷史。（The Defiant）[2023/3/7 12:46:33]

零知識證明對于確保許多加密協議的隱私和安全至關重要。它們是防止潛在信息泄露的保障，是Crypto世界的隱形防彈衣。該知識的應用可延伸至不同領域，包括區塊鏈技術和安全認證系統，其中敏感數據的保護是最重要的。

應用領域廣泛

區塊鏈及加密技術：像Zcash這樣的區塊鏈技術使用了零知識證明來保護交易隱私。一個人可以證明他們有足夠的Cypto貨幣來進行交易但又不透露其資金的確切數額。這保證了隱私的同時確保了交易的完整性。

身份驗證及認證：零知識證明還可以在不透露不必要的信息同時，用于確認身份。例如，一個人可以在不提供確切的出生日期的情況下證明他們已經超過18歲，或者在不分享密碼等敏感數據的情況下證明他們的身份。這最大限度地減少了盜取身份或未經授權訪問的風險。

Polygon以4億美元收購零知識初創公司Mir:金色財經報道，以太坊Layer2擴容解決方案Polygon宣布以4億美元收購零知識初創公司Mir，這筆交易是通過2.5億枚MATIC完成的。作為交易的一部分，Mir將更名為Polygon Zero，該項目將基于其ZK-proof技術構建一個ZK-rollup。Polygo聯合創始人Sandeep Nailwal在接受采訪時表示：“我們希望通過提供一系列解決方案，成為Web3平臺的AWS，使開發人員能夠在其上進行構建。”[2021/12/10 7:29:15]

安全多方計算（SMPC）：零知識證明可以促進多方之間的復雜互動，其中每一方都可以證明他們遵循商定的協議，而不透露其輸入的具體內容。這在如保護隱私的數據挖掘、安全投票系統等諸多方面都十分有效。網絡安全：零知識證明可以提供改進的安全協議，如安全密碼政策。其可以驗證用戶提出的密碼是否符合某些安全標準，而不讓服務器知曉或記錄實際密碼。因為密碼不會被儲存在任何地方，因此可以防止潛在的違規行為。保護隱私的同時共享數據：零知識證明可以用來證明某些數據符合特定的要求，而不透露數據本身，這在醫療或金融等領域尤其重要。這些領域對數據隱私的規定很嚴格，但以安全、保護隱私的方式分享信息或許會帶來巨大收益，比如促進醫療事業的發展等等。零知識證明已經在區塊鏈中釋放了新的技術可能性。這可以從ZKSync和Polygon的zkEVM等各種Layer 2中看到。然而，這僅僅是零知識證明創建的區塊鏈的一個子集。

Gate.io研究院發布“零知識證明于區塊鏈中的落地應用”報告:Gate.io研究院于今日發布“零知識證明于區塊鏈中的落地應用”報告。報告指出，在區塊鏈技術加快發展的背景下，多種應用場景應運而生，隨之而來的是用戶在隱私安全方面的更高需求。當前，眾多區塊鏈開發團隊提出了多種不同的用戶隱私安全保護機制。

其中，零知識證明與區塊鏈技術相結合作為一種新方案為提高區塊鏈隱私安全性提供了更多可能。該報告結合“零知識證明”的采納項目、區塊鏈系統“Zcash”的相關情況，對“Zcash”加密技術以及零知識證明進行了深入探討。 詳情點擊原文鏈接。[2020/6/28]

如何表示一個證明

在這一節以及文章的其余部分，我們將重點討論為基于PLONK證明系統構建的證明。

PLONK是一種零知識證明系統，其全稱是

“Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge”，即“基于拉格朗日基數的全局非交互式知識證明排列”。

從本質上講，PLONK是一個通用的、可更新的加密證明系統，這一創新允許在區塊鏈系統和其他分布式網絡中進行有效的驗證和擴展。PLONK背后的想法是構建一個通用的且可更新的證明系統。在零知識證明系統的背景下，“通用”意味著它可以被用于任何類型的計算；“可更新”則意味著加密參考字符串（用于生成和驗證證明的一段數據）可以隨著時間的推移安全地更新。

FMex已完成零知識證明開發工作:據了解，FMex目前已完成零知識證明開發工作，平臺啟動運營時將同步上線。通過零知識證明可實現平臺資產數據公開透明，不可偽造。屆時社區用戶可通過開源工具驗證資產數據。[2020/5/26]

PLONK因其高效和簡單性而引人注目，也因此成為了對安全、私密交易系統有需求的項目及公司的熱門選擇。與其他系統相比，它每個gate（計算的基本單位，我們下文統稱“門”）使用的約束條件更少，這使得計算速度更快且可擴展性更高。Vitalik Buterin已經發表了關于PLONK的更全面的描述。[復制下鏈接至瀏覽器即可查看原文https://vitalik.ca/general/2019/09/22/plonk.html]證明

在證明某個陳述前，我們先將該陳述用電路表示。一個電路將計算中的值與另外兩種類型的數據一起編碼：

1. 操作：比如對輸入數據進行的乘法和加法計算2. 操作執行的順序

為了編碼這些數據，PLONKish電路會被表示為一組向量和約束條件。約束條件是向量中單元必須遵守的關系，其中約束類型有：門約束和復制約束，他們分別表示電路中的操作和操作的順序。

采用不同的門和電路架構，有多種方法來表達電路。

將陳述表示為一個電路

假設我們有兩個門：一個乘法門和一個加法門。乘法門被表示為一個長度為3的向量|a|b|c|。如果這個門被選中，那么它將約束c等于a*b。同樣，加法門表示為一個長度為3的向量，如果選擇加法門，則c等于a+b。使用這些門，讓我們表示兩個向量（a,b）和（c,d）之間的點積。要做到這一點，我們需要完成以下計算：1. 使用乘法門計算a*b2. 用乘法門計算c*d3. 用加法門計算ab+cd這可以用向量來表示。

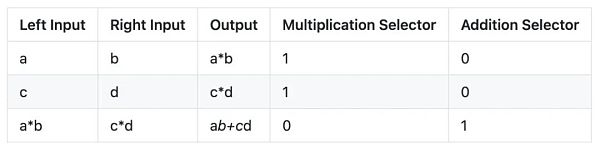
注意，第一個和第二個乘法門的輸出是加法門的輸入值。這個數據在我們的電路中是和門的約束條件分開編碼的。這被稱為復制約束。那么，為什么電路約束很重要呢？如果沒有約束，那么惡意驗證者就可以在電路中輸入他們喜歡的任何數值。例如，驗證者可以用aba*b替換ab+cd。與智能合約類似，約束條件在使用前必須通過證明系統得到驗證。證明陳述

現在我們可以用電路來表示陳述，那么證明者如何說服驗證者證明是有效的呢？對于PLONK系統來說，證明者必須讓驗證者相信門的約束和復制約束得到了實現。對于復制約束來說，這是通過進行排列組合檢查來實現的。

替換檢查是由Bayer-Groth首先提出的，然后由Gabizon、Williamson和Ciobotaru在PLONK論文中得到了進一步發展。為了證明門的約束，需要計算某個quotient polynomial（商的多項式）。

直觀地說，置換檢查表明，如果復制約束的條目被置換，電路仍然是相同的。置換檢查

如果對于b的所有第i個位置，存在與a相等的σ(i)位置，我們就說一個矢量a與矢量b之間是通過置換σ來關聯的。我們將其表示為σ(a)=b。給定兩個向量a=(a,b,...,c), b=(a',b',...,c')$, 和置換σ，我們想確定σ(a)=b。這可以按以下方法進行：

將向量表示為a'=((a,1),(b,2),...,(c,n))和b'=((a',σ(1),(b',σ(2)),...,(c',σ(n)) )。這是對關于置換σ的向量進行編碼。

將向量重寫為多項式向量：a''=((a+1X),(b+2X),...,(c+nX))和b''=((a'+σ(1)X), (b'+σ(2)X),..., (c'+σ(n)X))

檢查a''和b''作為多集是否等價，可以通過隨機選擇gamma來完成，從而顯示$(a+1X+γ)(b+2X+γ)....(c+nX+γ) = (a'+σ(1)X)+γ)(b'+σ(2)X+γ)....(c'+σ(n)X+γ)$ 。

通過隨機選擇一個β，我們可以通過Schwartz-Zippel lemma檢查這些多項式是否等價。如果它們作為多項式是等價的，那么集合a''和b''作為多集則是等價的。如果它們不是等價多項式，那么a''和b''就不是等價的多集。

CertiK中文社區

企業專欄

閱讀更多

區塊律動BlockBeats

曼昆區塊鏈法律

Foresight News

GWEI Research

吳說區塊鏈

西柚yoga

ETH中文

金色早8點

金色財經 子木

ABCDE

0xAyA

Tags：區塊鏈LONPLOPRO區塊鏈存證是什么意思WOOLONGUpload TokenCover Protocol

狗狗幣價格