智能合約增加隱私性并不簡單_ZKP:Cardence

對用戶來說，普通交易的隱私保護基本上算是一個已解決了的問題。如果我們想在不透露賬戶余額或轉賬金額的前提下轉移密碼學貨幣，我們有諸如大零幣或門羅幣這樣可接受的選項。不過，對于去中心化應用或者智能合約來說，隱私保護仍是一個尚未解決的問題。

是什么讓智能合約與普通交易在輸入/輸出的隱私保護上有所不同呢？

在本文中，我們將解密隱私保護從普通交易拓展到智能合約上會遇到哪些挑戰。為此，我們將考察應用于隱私幣的常用密碼學工具，并探討為什么這些工具不太適合更復雜的隱私應用。最后，我們將簡要介紹最近提出的一些智能合約隱私保護方案。

隱私保護的定義

「隱私保護」到底是什么意思？

我們將從函數的角度來定義隱私保護。例如，我們可以把?交易?看作是一些函數，它以賬戶余額和轉賬金額作為輸入。然后它輸出更新后的余額。

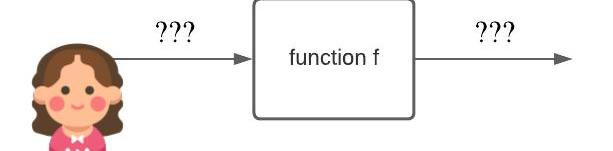
圖2：隱藏函數的I/O。

我們也可以考慮隱藏函數的調用者信息。有時候，函數輸入會留下關于函數調用者身份的線索。在實踐中，隱藏函數的輸入和輸出通常會和隱藏函數調用者的身份相結合。

圖3：隱藏函數調用者。

最后，我們可以考慮隱藏函數本身。這在密碼學貨幣領域不太常見，其通常與隱藏函數的輸入/輸出相結合。

某地址在3小時前買入約4.3萬枚RPL:5月15日消息，據推特用戶余燼監測，北京時間5月15日06:18:59，0xc965開頭地址從幣安轉出1202枚ETH（約216萬美元），后將ETH換成42,626枚RPL，均價為50.75美元。過去24小時，幣安上的RPL/USDT成交量為272萬美元。此外，該地址于昨日新創建。[2023/5/15 15:03:20]

圖4：隱藏函數本身。

當你在本文中看到「隱私保護」這個詞時，請把它當成一個總稱，指的是?至少支持I/O隱私保護?的東西。

好吧，但我們要在哪里用到隱私保護呢？

我們可以認為普通交易的隱私保護已被解決，所以讓我們直接轉到智能合約的隱私保護。

不過，我們先繞個彎子，回顧一下以太坊……

以太坊支持用戶自定義的合約，合約以代碼的形式執行。這些合約用以太坊自己的圖靈完備的語言編寫，每執行一個操作都要支付一些費用。因此，每筆交易都要附上交易費，以激勵礦工打包交易。

應用的隱私保護

智能合約讓我們在區塊鏈上得以構建豐富的應用——從用戶可交易各種密碼學貨幣及其衍生品的去中心化交易所，到允許權益持有者對提案進行投票的去中心化自治組織。

我覺得沒必要長篇大論講解為什么DAO需要隱私保護；在現實生活中，投票通常都是私下進行的，所以想要隱藏我們的虛擬投票也是非常合理的。

數據：今日有三個地址通過 Uniswap V3 出售了近 9000 枚以太坊:金色財經報道，據 Lookonchain 監測，今日 idl.eth、maxkordek.eth 以及開頭為 0x6c1A 的地址共在 Uniswap V3 上賣出了 8988 枚以太坊。[2023/2/14 12:04:45]

另一方面，去中心化交易所的隱私保護需要解釋一下。搶先交易無論是對中心化交易所還是去中心化交易所都是一個問題。在區塊鏈世界里，搶先交易者密切觀察已提交的訂單，并通過支付更高的交易費實現插隊。這使得搶先交易者Eve能夠搶在Bob之前買到Bob想買的證券，并隨后以更高的價格賣給Bob。封閉式拍賣是解決這個問題的一個可能的辦法。對于有興趣的讀者，可以在這里找到更多關于在去中心化交易所的搶先交易的信息。

不過，以太坊的智能合約并沒有提供任何形式的開箱即用的隱私保護。所有的信息都是公開可查看的——合約的輸入/輸出，合約的功能，參與的用戶，等等。為以太坊的智能合約?添加?隱私保護不是一件容易的事情，因為以太坊從一開始就沒有被設計成支持隱私保護。雖然在以太坊上可以實現隱私交易，但是更復雜的隱私保護操作往往過于昂貴，甚至超過以太坊單個區塊的費用限額，以至于無法實現。

難道我們就不能設計一種新的密碼學貨幣，從一開始就支持任何函數的隱私保護嗎？畢竟，大零幣和門羅幣就是這樣做的。

目前我們還不清楚如何在密碼學貨幣中支持任意函數的I/O隱私保護。為了理解這些挑戰，我們需要考察密碼學貨幣是如何支持隱私交易的。

通往隱私保護之路

Cardano創始人指責Gemini：不將ADA上市與破產風險“密切相關”:金色財經報道，Cardano創始人Charles Hoskinson指責由Winklevoss雙胞胎創立的加密貨幣交易所Gemini拒絕添加ADA加密貨幣。Hoskinson認為，不將ADA上市與破產風險“密切相關”。

FTX是上個月破產的第二大加密貨幣交易所，沒有任何現貨ADA對。在FTX倒閉前幾周，創始人SBF在推特上表示，添加代幣已在交易所的路線圖上。值得注意的是，ADA是沒有在FTX現貨上市的加密貨幣。[2022/12/5 21:22:31]

我們先考察用于普通交易?I/O隱私保護的密碼學工具。我們將關注賬戶模型而非UTXO模型的加密貨幣。賬戶模型在支持智能合約的場景下尤其有用，不過賬戶模型對于隱私計算來說不是必須的。

工具1：同態加法

大多數密碼學貨幣的隱私保護方案都依賴于具有?加法同態?的加密或承諾方案。為了簡單起見，我們將專注于加密方案，但同樣的原則也適用于承諾方案。

在加法同態加密方案下，我們有以下等式：Enc(a)+Enc(b)=Enc(a+b)。

因此，加法同態加密方案允許任何人?這樣驗證交易的有效性：Enc(balance)+Enc(transferamount)=Enc(balance+transferamount)?。

Upbit暫停Serum(SRM)存款服務:11月14日消息，韓國加密貨幣交易所Upbit發布公告稱，由于Serum（SRM）價格波動性加大，市場價格與其他交易所存在差異，將暫時停止支持SRM存款服務。

據悉，11月10日Upbit發布關于限制加密資產提款至FTX交易所的通知，Upbit稱由于FTX交易所的內部情況，已暫停用戶提款至FTX的交易。[2022/11/14 13:00:46]

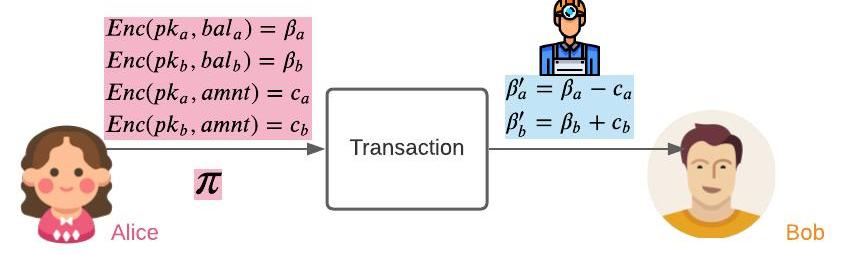
圖6：現在給隱私交易附上必要的ZKP?

Alice用她和Bob的公鑰分別對轉賬金額進行加密，得到了c_a和c_b。她提供了一個ZKP，π，證明她在交易中沒有作弊。礦工們會驗證所有的必要條件是否被滿足，ZKP是否有效。然后，他們會使用同態加法分別更新Alice和Bob的加密余額：β_a=β_a-c_a，β_b=β_b+c_b。注意，雖然用戶提供了加密后的輸入和一個ZKP，但是礦工需要負責執行計算以及更新加密后的余額。在區塊鏈中，我們假設大多數礦工是誠實的，所以我們知道他們會正確地更新Alice和Bob的余額。

注：這是一個大大簡化的解釋

將普通交易的隱私保護技術拓展到智能合約上面臨的挑戰

所以我們剛剛已經看到了，我們可以執行隱藏輸入和輸出的交易。那么我們可以把在隱私交易中用到的技術，用于支持應用的I/O隱私保護嗎？換句話說：

隱私計算和隱私交易是否不同？如果是，為什么？

問題1

需要注意的是，隱私交易需要滿足設定的條件才是正確的。我們如何能弄清楚一個任意的合約需要滿足哪些條件？這些條件顯然受特定的應用影響。在投票中，我們可能希望證明我們隱藏的投票是在正確的范圍內進行的，而對于拍賣，我們可能希望證明我們的賬上有足夠的資金用于封閉投標。

游戲驛站漲超13%:金色財經報道，數據顯示，游戲驛站(GME.US)漲超13%，報101.105美元。該公司周一表示，將為NFT和加密貨幣推出數字錢包。公司將其新錢包描述為自我托管的以太坊錢包。該錢包的網絡瀏覽器擴展插件可以從Chrome Web Store下載。[2022/5/26 3:41:58]

對問題1的潛在解決方案

這個問題也沒那么嚴重；只是需要用戶做更多的工作。去中心化應用的開發者必須明確他們的特定應用需要滿足哪些條件，并將這些條件傳達給用戶。為了能夠證明各式各樣的條件，我們可能希望在方案中支持一些通用的ZKP。所謂?通用?的ZKP就是能夠證明任意的聲明。

問題2

在普通交易中，我們只對屬于同一個用戶的值進行操作。比如在圖6中，礦工把用Alice的公鑰加密后的余額與用Alice的公鑰加密后的轉賬金額相加。如果我們想對屬于不同用戶的輸入值進行隱私計算呢？這并不是一個多么牽強的需求，比如我們考慮對投票做隱私保護時就會涉及。

對問題2的潛在解決方案

目前還不清楚如何在用戶相互之間不透露輸入明文的情況下，支持對不同用戶的輸入進行計算。有一些先進的密碼學元件，允許用戶對不同密鑰加密的輸入進行計算。然而，這些方案的成本都非常高，而且有很多缺點。在密碼學貨幣的應用場景下，目前似乎沒有人有一個很好的解決方案來解決這個問題。

問題3

普通交易只需要同態加法，因為我們只需要將加密的轉賬金額加到加密的余額上。如果我們想進行更復雜的計算，可能涉及到乘法呢？

對問題3的潛在解決方案

同態乘法允許我們將加密的輸入相乘，使得?Enc(a)*Enc(b)=Enc(a*b)?。通過同態加法和同態乘法，我們可以表示任意多項式函數。所以，我們很自然地想到這個問題：

我們能夠支持同態乘法嗎？

一個既能支持同態加法，又能支持同態乘法的加密方案是全同態加密。使用FHE，我們仍然可以遵循圖6中所描繪的模型。也就是，用戶指定加密輸入，要運行的函數，以及證明加密輸入滿足必要條件的ZKP。礦工能夠驗證ZKP。他們使用同態加法和同態乘法直接對用戶提供的密文進行操作。

不幸的是，FHE方案使用基于格的加密技術，這與密碼學貨幣中使用的超高效的ZKP并不兼容。我們曾經寫過關于FHE及其問題的文章。目前，由于FHE存在一些缺點，還沒有人提出基于FHE的解決方案。

這樣，我們目前就只剩下兩種方法來解決問題3了。

接受我們只能支持同態加法的現狀，遵循隱私交易模型。

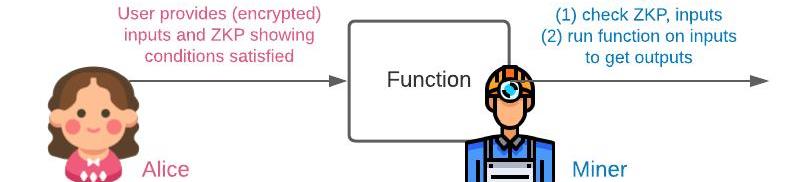
圖7：遵循隱私交易模型?

在這里，用戶提供加密后的輸入和一個ZKP，證明他們的輸入滿足特定應用的一些指定條件。礦工驗證證明，使用同態加法對輸入進行操作。需要注意，應用于輸入的函數只能用加法來表示。因此，只要函數只需要用到同態加法，我們就可以要求礦工對我們加密的輸入執行任意滿足該條件的函數。這就是?Zether?所采用的方法。

要求用戶線下計算。這樣我們就不需要為加密/承諾支持同態乘法了。

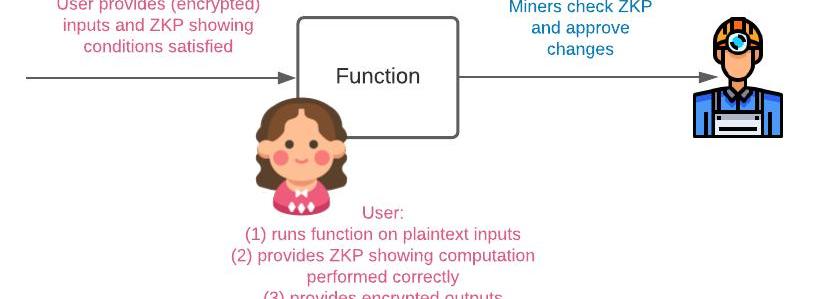
圖8：將工作外包給用戶

在這里，我們要求用戶Alice將對明文的幾乎所有計算都放到線下進行。她會公布計算的加密輸入和加密輸出。因為計算是在線下完成的，她同樣需要提供一個ZKP證明計算過程是正確的。注意，這一步對隱私交易來說是不必要的，因為礦工會執行計算，而我們假設大多數礦工是誠實的。就應用而言，她可能還需要另一個ZKP，證明應用指定的條件已被滿足。礦工所需要做的就是驗證ZKP是否有效，然后同意Alice提出的狀態變更。這就是?Zexe?和?Zkay?所采取的辦法。

我不會在這里討論哪種方法更優；只想說明它們是不同?的。

智能合約的隱私保護

前面我們已經談到了在區塊鏈中支持任意函數的隱私保護要面臨的一些問題，現在讓我們來看一看一些已有方案的構造。

如果前面說得還不夠清楚，我再重申一下，這個領域距離解決問題還有很長的路要走。設計這些構造的論文都是在過去兩年中發表的。

Zether是一個建立在以太坊上的隱私交易方案。它可以延伸到支持有限的智能合約的I/O隱私保護——即那些可以通過同態加法表示的合約。這使得我們可以執行簡單的封閉式拍賣和隱私投票。遺憾的是，由于gas的限制，目前在以太坊上只能實現在交易中隱藏用戶余額和轉賬金額。與接下來的兩種構造不同，Zether使用的是「透明」的ZKP。

Zkay同樣延伸了以太坊的設計以支持智能合約的隱私保護。他們依賴ZKP保障隱私計算的正確性，從而可以將大部分工作丟給用戶在線下完成。因此，這種設計選擇使得它們能夠支持比Zether更多類型的函數。

Zexe則試圖延展大零幣的設計，以支持任意腳本。與前兩者不同，Zexe還可以支持函數本身的隱私保護。

*Zkay和Zexe使用的是帶有可信設置的ZKP方案。不過，這些ZKP方案當然可以被不需要可信設置的方案替代。**在區塊鏈的場景中，I/O隱私保護似乎比函數隱私保護更有意義，因為用戶很可能希望在決定是否參與合約之前先對合約進行審計。請注意，還有其他一些用于智能合約隱私保護的構造，但是這些方案都需要某種準-受信任的管理器或受信任的硬件。

大多數智能合約的隱私保護方案都需要額外的安全假設——無論是受信任的啟動設置，準-受信任的管理器還是受信任的硬件。然而，ZKP是一個快速發展的領域，更高效透明的構造很可能會被創造出來。

期許

當涉及表達能力，信任和效率時，在智能合約的隱私保護上進行的探索提出了很多有趣的理論和實踐挑戰。現在，很難說在圖7或者圖8所代表的方法中，哪種可能會在區塊鏈的隱私計算中勝出。此外，未來全同態加密的進展能否轉化到區塊鏈中以解決問題3，這也是一個很有趣的看點。

原文標題：《干貨|要給智能合約增加隱私性并不簡單》

來源：金色財經

Tags：ZKP以太坊ENCETHZKPEPE以太坊硬幣交易所交易時間CardenceTAIKULAETH

酷幣